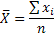Ecuaciones e identidades

Una igualdad entre expresiones algebraicas es una relación del tipo A=B, siendo A y B expresiones algebraicas que en principio podemos suponer dependientes de la variable x, A(x) y B(x). Por ejemplo 3x-4=(7x^2+3)/4.

La cuestión es que la igualdad puede ser cierta para todo x, en cuyo caso tenemos una identidad, o para algunos valores de x, en cuyo caso tenemos una ecuación. Pero también puede que no sea cierta para ningún valor de x, en cuyo caso, es una igualdad falsa. Las identidades se usan para definir las propiedades algebraicas fundamentalmente, por ejemplo la distributividad, 3(x+2)=3x+6. Si intentamos resolver una identidad como una ecuación llegamos a la expresión 0=0. En este caso concluiríamos que la posible ecuación tiene infinitas soluciones. Si intentamos resolver una igualdad falsa como una ecuación, por ejemplo 3x+5=3x-8, llegamos a un absurdo numérico, como en el ejemplo anterior nos daría 5=-8. También puede ocurrir que tengamos ecuaciones que no podamos decidir si tiene o no solución, porque no tenemos método para resolverla, o bien, puede ocurrir que en un campo numérico no tengamos solución pero en otro sí, por ejemplo x+3=0, no tiene solución para los naturales pero sí para los enteros.
Para resolver una ecuación A(x)=B(x), lo que haríamos es utilizar identidades que sustituyan ambas partes por expresiones cada vez más simples, A1(x)=B1(x), siendo A(x)=A1(x) y B(x)=B1(x) identidades; y quitarmos finalmente dos expresiones idénticas en ambas partes, A1(x)-A2(x)=B1(x)-B2(x), siendo A2(x)=B2(x) una identidad, de forma que nos quede la igualdad simple x=a.
Por ejemplo:
3(x-4)+7=4(x-2)
Usamos las identidades 3(x-4)=3x-12 y 4(x-2)=4x-8 para sustituir y tenemos,
3x-12=4x-8
Restamos la identidad 3x-8=3x-8 en ambas partes y tenemos,
-4=x, o bien, x=-4

Unidad didáctica: Poner un suelo

Motivación:

Bricolaje Decoración

Una habitación cuadrada de 36 m² se va a recubrir usando losas cuadradas de 1.60 m² cada una (las medidas son aproximativas a escala de centésimas). ¿Cuántas losas se necesitan?

Experimentación:
Empezamos a poner losas:

2 losas: 36-2·1.6=36-3.2=32.8 m²  faltan por cubrir
3 losas: 36-3·1.6=36-4.8=31.2 m²  faltan por cubrir
...............................
10 losas: 36-10·1.6=36-16=20 m²  faltan por cubrir
..............................
20 losas: 36-20·1.6=36-32=4 m²  faltan por cubrir
.............................
23 losas: 36-23·1.6=-0.8 m²  sobran

Conceptualización:
Como la habitación es cuadrada y las losas también los son, formamos grupos de losas que sean cuadrados perfectos:

1 losa (1x1): 36-1.6=34.4 m² faltan por cubrir
4 losas (2x2): 36-1.6·4=36-6.4= 29.6 m²
..............................
16 losas (4x4): 36-1.6·16=36-25.6=10.4 m²
Los 10.4 m² que faltan hay que rellenarlos de otra forma, hay que partir losas.

Procesamiento:
16 losas son un cuadrado de 4x4 losas. La habitación tiene de lado 6 m y cada losa la raíz de 1.6, aproximadamente 1.2 m si hacemos un redondeo inferior (perdiendo unos 0.06 m=6 cm). Entonces, las cuatro losas son 4·1.2=4.8 m, cabe otra losa rebajando un poco, 5·1.2=6. Entonces el total de losas será 16+4+4+1=25. Si hacemos esto añadimos 2 losas más. Si corregimos el redondeo con dos cifras, el lado es 1.25 m, 4·1.25=5 m. Hay que recortar las últimas para hacer 8 cuadrados de 1x1, y con lo que sobra se ahorra una losa si usamos los recortes para hacer la última. Aún así son 24 y el resultado queda poco estético.

Mecanización:
Asumimos que las losas son de 1.25 m de lado, por tanto con cuatro losas por lado son 5 m y falta 1 m para los 6 m. Si partimos las losas grandes en losas cuadradas más pequeñas, pero lo más grandes posible, tienen que tener de lado un divisor de 100 cm y de 125 cm, es el máximo común divisor de ambos números:
mcd(100,125)=25
Las losas grandes se cortan en losas cuadradas de 0.25 m de lado y cada losa da 25 losas cuadradas más pequeñas de 0.0625  m²  . Para rellenar todo el espacio se necesitan 36:0.0625=576, 576:25=23.04 losas, serían por tanto 24 losas. Aunque se podría ajustar para obtener las 23 losas, cabe pensar que no es posible en la práctica obtener precisión de milímetros para hacer cortes.

Consolidación:
Ante el problema de recubrir una habitación cuadrada (de lado L en m) usando losas cuadradas (de lado l en m) de forma que obtengamos un resultado estético, procederemos de la siguiente manera:
1º) Dividir L² entre l², si no es exacta tomar el redondeo superior como primera aproximación del número de losas. Si es exacta, el cociente es el resultado buscado.
2º) Dividir L entre l, tomar el cociente entero, ci=Ent(L/l). El número de losas máximo es ci·ci+2ci+1.
3º) Si es posible dividir en cuadrados más pequeños las losas cuadradas y el recubrimiento es aceptable usando el máximo tamaño posible, calcular en cm el mcd(l , L-ci·l)=d.  Hay que cortar las losas en cuadrados de lado d cm. El número de losas pequeñas que salen de una grande es l²:d²=n, con l en cm
4º) El número final de losas grandes es el redondeo superior de (L²:d²):n, o sea, Ent(L²/l²)+1

Evaluación:
¿En qué casos se debe de dividir la losa en cuadrados y en qué casos es suficiente con rebajar la última fila y columna?
Si hay que dividir la losa en cuadrados más pequeños de lado d, este valor debe de ser suficientemente grande para que no queden losas demasiado pequeñas. Pero si hay que rebajar la última fila y columna debe de quedar suficientemente recortado para que no quede mal.
El número de losas necesarias N siempre cumplirá:

[Ent(L/l)]²<=N<=[Ent(L/l)+1]²

[Ent(L/l)]²<=Ent(L²/l²)+1<=[Ent(L/l)+1]²

Problemas cotidianos - el tráfico

Otra de las fuentes habituales de problemas matemáticos está en el tráfico de las ciudades. Para un ciudadano que está acostumbrado a circular por la ciudad siguiendo una misma ruta, puede encontrarse un día con que el trayecto habitual está cortado, que están realizando un determinado evento que impide pasar por un tramo del trayecto, entonces, ¿cómo buscar un nuevo trayecto óptimo?.

Por ejemplo, consideremos un segmento del plano de la ciudad, con sus direcciones, como el de la figura siguiente:

Si el conductor tiene que ir de A a F y está cortado el tramo BF, ¿qué trayecto debe seguir que le lleve el menor tiempo posible?.

Problemas de la vida cotidiana

¿Qué problemas matemáticos podemos tener en el día a día?

http://motor.terra.es/addon/img/1f2898parking_598p.jpg

Por ejemplo, todos podemos recordar haber escuchado a alguien decir que se había perdido al ir a recoger el coche en el aparcamiento del centro comercial (CC). ¿Podemos usar las matemáticas para encontrar el coche en el aparcamiento?. Normalmente hay dos indicativos, el número de plaza y el color de la plaza. El número podemos olvidarlo y el color también, podemos no habernos fijado suficientemente en él. También tenemos toda una serie de pistas que podrían ayudar, desde un coche próximo que nos llamó la atención hasta un cartel que había cerca y que anunciaba determinado producto. En última instancia tenemos información de por dónde estamos entrando en el aparcamiento y, tal vez, por dónde entramos en el centro comercial desde el garaje.
Supongamos que en un aparcamiento de un CC hay 4 plantas de garaje, cada una con 100 plazas de aparcamiento. La primera es azul (0-99), la segunda en verde (100-199), la tercera roja (200-299) y la cuarta amarilla (300-399). Una persona no sabe dónde dejo su coche, recuerda que el color era azul o verde y que su plaza acababa en 8, ¿qué estrategia debe seguir para buscarlo?

En principio tiene dos plantas donde buscar, la azul y la verde, en total 200 plazas. Dentro de ellas, que terminen en 8 hay 10 para la azul y 10 para la verde, por tanto tiene que buscar como mucho 20 opciones de un total de 200. Es el 10% de las plazas de las dos plantas, que es el 5% de las plazas de todo el garaje. Si durante la búsqueda alguna pista nos reafirma en el color de la planta, optimizamos la búsqueda buscando en una sola planta, reduciendo así las opciones a buscar en el 2'5% del total de plazas del aparcamiento. Si otra pista nos permite dividir la planta en dos mitades y buscar solo en una de ellas, pasaríamos al 1'25%, y así sucesivamente hasta llegar al 0%. Es la estrategia de dividir y vencer.

Motivaciones para aprender matemáticas

La motivación tiene que ver con la posibilidad de hacer real lo deseado.  Hace siglos, cuando las sociedades eran agrícolas, las matemáticas tenían aplicaciones prácticas que estaban al alcance de muchos de los ciudadanos como por ejemplo medir una superficie de terreno, calcular la cantidad de semillas necesarias para hacer la siembra, diseñar canales de regadío, hacer molinos para aprovechar la fuerza del aire o del agua,... Hoy en día la sociedad es más sofisticada, la mayoría de los habitantes viven en las ciudades, manejan intuitivamente mucha tecnología pero solo como usuarios sin comprender ningún fundamento, es una sociedad de consumo en la que lo que se estropea se cambia por otro aparato nuevo y normalmente no hay mucha necesidad de crear algo nuevo. Los trabajadores altamente cualificados y profesionales universitarios sí necesitan conocimientos matemáticos para dominar sus profesiones. También es cierto que mucha de la información que hay en la prensa está en términos cada vez más matemáticos, sobre todo estadísticos, lo que ayuda a mejorar el nivel de formación matemática de los ciudadanos. En general, podemos decir que para el ciudadano medio no hay muchas posibilidades de plantearle problemas matemáticos reales que le haga motivarse en el reto de resolverlos con la consiguiente satisfacción de conseguirlo y, por tanto, desarrollar el gusto de aprender.

Unidad Didáctica: La ecuación de 2º grado

«El hombre, dicen, es un animal racional. No sé por qué no se haya dicho que es un animal afectivo o sentimental. Y acaso lo que de los demás animales le diferencia sea más el sentimiento que no la razón. Más veces he visto razonar a un gato que no reír o llorar. Acaso llore o ría por dentro, pero por dentro acaso también el cangrejo resuelva ecuaciones de segundo grado.» Unamuno, Del sentimiento trágico de la vida

UNIDAD DIDÁCTICA: La ecuación de 2º grado 


(MOTIVACIÓN)
Juan tiene una parcela de terreno rectangular de 6m de largo por 5m de ancho, limitada por la parcela de Antonio como se ve en el gráfico. Juan necesita tener una parcela cuadrada por lo que acuerda con Antonio el recortar el largo de su parcela dándosela a Antonio y aumentar la misma superficie al ancho con el terreno que a cambio le de éste, de tal forma que consiga una parcela cuadrada. ¿Cuánto deben de recortar al largo y aumentar al ancho para que intercambien los mismos metros cuadrados?

Puesto que la parcela final es cuadrada: 
6-x=5+y,  y=1-x
Puesto que los terrenos intercambiados tienen el mismo área:
5x=(6-x)y, 5x=(6-x)(1-x), 5x=6-6x-x+x², x²-12x+6=0
Necesitamos resolver una ecuación de segundo grado.

(EXPERIMENTACIÓN)
En el caso concreto del problema podemos ir quitando poco a poco al largo del rectángulo y probamos si puede ser el ancho igual para formar el cuadrado comprobando si el área es 30.
x=0.1, largo=5.9, ancho=5.9, 5.9·5.9=34.81>30
x=0.2, largo=5.8, ancho=5.8, 5.8·5.8=33.64>30
x=0.3, largo=5.7, ancho=5.7, 5.7·5.7=32.49>30
x=0.4, largo=5.6, ancho=5.6, 5.6·5.6=31.36>30
x=0.5, largo=5.5, ancho=5.5, 5.5·5.5=30.25>30
x=0.6, largo=5.4, ancho=5.4, 5.4·5.4=29.16<30
La solución es un cuadrado cuyo lado está entre 5.4m y 5.5m

(CONCEPTUALIZACIÓN)
Si hemos recortado x en el largo entonces tenemos un cuadrado de lado 6-x, cuyo área tiene que ser 5·6=30, entonces la ecuación es:
(6-x)²=5·6, que despejando el cuadrado da:
6-x=(+/-)raíz(5·6), esto es, la media geométrica de los lados del rectángulo.
x=6(+/-)raíz(5·6), y=-5(+/-)raíz(5·6)

(PROCESAMIENTO)
Para resolver la ecuación x²-12x+6=0 hay que convertir esta en un cuadrado perfecto y pasar la parte numérica sobrante al segundo miembro.
x²-12x+6=x²-2·6x+36-30=(x-6)²-30=0
(x-6)²=30, x=6(+/-)raíz(30)

(MECANIZACIÓN)
Si consideramos los coeficientes como datos podemos obtener la fórmula que permite encontrar las soluciones:
a=1, b=-12, c=6
x²+bx+c=0
(x+b/2)²-(b/2)²+c=0
x+b/2=(+/-)raíz[((b/2)²-c]
x=-b/2(+/-)raíz[((b/2)²-c]
x=[-b(+/-)raíz[b²-4c]]/2
x=[12(+/-)raíz[144-24]]/2=(+/-)0.522.....
Si a es distinto de 1 se divide la ecuación por a, 
ax²+bx+c=0
x²+b/ax+c/a=0 y sustituyendo en la fórmula anterior se tiene la fórmula cuadrática general
x=[-b(+/-)raíz[b²-4ac]]/(2a)

(CONSOLIDACIÓN)
Entonces ante una ecuación de segundo grado ax²+bx+c=0 para resolverla hemos seguido el método de completar cuadrados:
Por ejemplo 2x²-6x-10=0
1) Dividimos la ecuación por el coeficiente a, en este caso 2
(2x²-6x-10=0):2---->x²-3x-5=0
2)  Cambiamos el coeficiente de x multiplicando y dividiendo por 2
x²-2(3/2)x-5=0
3) Sumamos y restamos el cuadrado del número que está multiplicado por 2 en el coeficiente de x
x²-2(3/2)x+(3/2)²-(3/2)²-5=0
4) Expresamos el cuadrado del binomio con los tres primeros términos y simplificamos los últimos y lo pasamos al segundo miembro
(x-(3/2))² =29/4
5) Despejamos el cuadrado
x=(3/2)(+/-)raíz(29/2)

(EVALUACIÓN)
Se ha encontrado un método general que resuelve cualquier ecuación de segundo grado. En la práctica se utiliza la fórmula cuadrática con los coeficientes a, b y c de la ecuación. Como la solución depende de la raíz, si el radicando es negativo no hay solución real. Si llamamos discriminante al radicando D=b²-4ac, tenemos el siguiente criterio sobre la existencia de soluciones:
Si D=0 hay una sola solución que se dice doble
SI D<0 no hay solución real
Si D>0 hay dos soluciones reales y distintas
Lo que se necesita es ampliar el dominio de los números reales para que siempre exista solución.

El ciclo de aprendizaje 2

Cada fase del ciclo utiliza un aspecto de las matematicas, así:

MOTIVACIÓN --> RELACIONES
EXPERIMENTACIÓN --> CÁLCULOS
CONCEPTUALIZACIÓN--> PROPIEDADES
PROCESAMIENTO --> FUNCIONES
MECANIZACIÓN --> FÓRMULAS
CONSOLIDACIÓN --> MÉTODOS
EVALUACIÓN --> CRITERIOS

La desigualdad triangular, un criterio

La desigualdad triangular es un criterio que dice que en cualquier triángulo la suma de dos de sus lados es mayor o igual que el tercero.

a+b>=c

Es evidente, si suponemos que los vértices A, B y C son pueblos de un mapa, y los lados, a, b y c, son carreteras rectas entre los pueblos, comprendemos que ir de A a B recorriendo c km es más corto que ir primero de A a C, recorriendo b km, y, luego, de C a B, recorriendo a km.

Es un criterio porque sirve para comprobar si es posible tener un triángulo con determinadas dimensiones de sus lados. Por ejemplo, un triángulo cuyos lados sean a=6, b=3, c=2, no puede existir porque 3+2<6. Sin embargo un triángulo con a=7, b=5, c=10, sí existe porque en cualquier combinación que hagamos se cumple la desigualdad triangular:

7+5>=10; 7+10>=5; 5+10>=7

Un viaje algebraico en guagua

Suponemos la linea 1 de guaguas de la ciudad que va de A a E, parando en B, C y D (simplificando). La línea es de ida y vuelta, cuando llega a E vuelve hacia A parando en los mismos puntos. Un pasajero no tiene por qué bajarse en el principio o final de línea, puede continuar. Tenemos las siguientes operaciones que puede hacer un pasajero que sube a la guagua:

1. Subir en una parada y bajar en otra. Si x son las paradas que recorre, entonces está garantizado que acaba en una parada
2. También puede no subir cuando llega la guagua. Sería la operación nula.
3. Si va de un punto a otro, puede tomar la de vuelta y retornar al punto de partida. Si recorre x paradas, al recorrer las mismas en sentido opuesto, -x, vuelve al mismo sitio.
4. Puede asociar de distintas formas tres trayectos consecutivos llegando siempre al mismo punto. Si recorre primero x paradas, después y, y después z, el resultado final es el mismo contabilizado como (x+y)+z=x+(y+z)
5. El recorrido es conmutativo. Si recorre primero x paradas y luego y paradas, es lo mismo que si recorre primero y paradas y después x, x+y=y+x.

Estamos ante una estructura de grupo conmutativo.

Una estructura algebraica

Un conjunto con una operación interna que cumple una serie de propiedades tiene una estructura algebraica. 

Pongamos por caso que Luis tiene un cerdito en el que añade monedas de un euro (por simplicidad) aunque algunas veces quita algunas monedas. Cuando no tiene que quitar recurre a su padre aunque adquiere una deuda.

Veamos el estado en que se encuentran las finanzas de Luis según su cerdito:
Necesitamos los números enteros para llevar la contabilidad. La operación que hace es echar monedas de un euro, la suma de positivos, pero también quita monedas, la suma con negativos. Esta operación siempre tiene sentido si suponemos que el cerdito puede llegar a contener ingentes cantidades de dinero, y también, que él puede quitar aunque no haya nada pidiendo dinero a su padre contrayendo una deuda todo lo grande que se quiera (al menos en teoría). La operación también es conmutativa, es lo mismo echar cuatro euros y después siete, que echar siete y después cuatro. La operación nula es ver el cerdito sin sacar ni meter nada. Y puede echar tres y cuatro monedas juntas y, más tarde, cinco, obteniendo el mismo resultado que si echa tres y, más tarde, cuatro y cinco, conjuntamente.

Las finanzas de Luis en su cerdito siguen una estructura algebraica, que podemos llamar "grupo conmutativo"

Supongamos ahora que Luis ya es mayor y tiene una cuenta corriente en el banco haciendo las operaciones de meter o sacar dinero por un cajero automático. Este debe de operar con las imposiciones o extracciones siguiendo la estructura de grupo conmutativo:

• Cada imposición o extracción queda reflejada con un saldo en positivo o en negativo.
• Puede operar en el cajero para ver el estado sin por ello modificar su saldo total.
• Lo que ingresa lo puede sacar y queda igual, o viceversa.
• Las operaciones se pueden asociar de distinta manera importando solamente el resultado neto final.
• El orden de las operaciones no influye en el saldo final.

La propiedad conmutativa

Consideremos los números reales y sus siete operaciones. Una operación es conmutativa cuando da el mismo resultado si la realizamos en orden inverso sean cuales sean los números empleados.

• La suma es conmutativa: a+b=b+a, por ejemplo, 3+5=5+3
• La resta no es conmutativa: 6-5<>5-6. Sólo se cumple la conmutatividad cuando el número es el mismo, por ejemplo 4-4=4-4.
• El producto es conmutativo: a*b=b*a, por ejemplo, 6*9=9*6
• La división no es conmutativa: 6/4<>4/6. Sólo se cumple cuando los números son iguales, 8/8=8/8, o son opuestos, 5/(-5)=(-5)/5.
• La potencia no es conmutativa: 5²<>2⁵. Pero, ¿qué pares de números cumplen esa propiedad? Si son iguales se cumple. Sabemos, por ejemplo, que el 2 y el 4 la cumplen también, 2⁴=4².
• La raíz y el logaritmo tampoco son conmutativas. ¿Existen pares de números no iguales que sean conmutativos para esa propiedad?

Propiedades que generan propiedades

La notación normativa o estándar de un polinomio de segundo grado es ax²+bx+c. Aunque un polinomio de segundo grado puede escribirse como a(x-r)(x-s), donde r y s son las  llamadas raíces del polinomio, que por la propiedad distributiva se puede expandir como ax²-asx-arx+ars, que se puede contraer en parte aplicando la distributiva de forma inversa como: ax²+a(-r-s)x+ars. Comparando ambas expresiones se tiene que:
r+s=-b/a; rs=c/a.,
que son las propiedades de la suma y el producto de las raíces de un polinomio.

Reglas vs fórmulas

La solución de una ecuación de segundo grado, ¿fórmula o regla?
Bueno, x=(-b+-raiz(b^2-4ac))/(2a), parece más bien una fórmula porque:

• En primer lugar tiene carácter práctico, da las soluciones de la ecuación, la fórmula se demuestra una sola vez y ya se puede aplicar.
• Hay que sustituir las letras por los coeficientes a, b y c de la ecuación, de forma constructiva.
• Permite separar las ecuaciones con solución de las que no la tienen según el discriminante.

El cuadrado del binomio, ¿regla o fórmula?

Bueno, (a+b)^2=a^2+2ab+b^2, parece más bien una regla porque:

• Tiene una letanía para acordarse, "el cuadrado del primero, más doble producto del primero por el segundo, más el cuadrado del segundo"
• Nos aligera de tener que hacer el producto (a+b)(a+b).
• Se usa para expandir la expresión.

Propiedades vs reglas

¿La propiedad conmutativa o la regla conmutativa?
Bueno, parece que es más propiedad que regla: a(op)b=b(op)a.

• En primer lugar es general para muchas operaciones, como la suma o el producto de reales. (compara parecidos)
• En segundo lugar es opcional el uso y depende de la conveniencia del momento.
• En tercer lugar indica lo que podemos o no podemos hacer. Por ejemplo no podemos aplicarla en el producto de matrices.

¿La regla del producto de derivadas o la propiedad del producto de derivadas?
Bueno, parece más la regla del producto: f=g·h==>f'=g'·h+g·h'

• En primer lugar es particular, indica como hacer la derivada de un producto, es expansiva.
• En segundo lugar aligera la operatoria puesto que nos evita estar con límites.
• En tercer lugar se memoriza con una frase: la derivada del primero por el segundo sin derivar, más, el primero sin derivar por la derivada del segundo.

Funciones elementales

Las funciones elementales son los objetos más simples del análisis. La primera función que se considera como tal es la función constante, f(x)=k, siendo k un número. Por ejemplo f(x)=6. La siguiente función elemental es la identidad f(x)=x. A partir de aquí se pueden operar estas funciones para obtener nuevas funciones. Por ejemplo, la suma repetida de funciones identidad da otra función elemental, la función afín: f(x)=x+x+x+x=4x. La suma de la función afín con la función constante da la función lineal, por ejemplo f(x)=4x+6. La multiplicación repetida de la función identidad da la función potencia, f(x)=x*x*x=x³. La suma repetida de funciones potencia o la multiplicación de la función constante por la potencia da una función monomio, por ejemplo f(x)=6x³. Finalmente, la suma de funciones monomio da la función polinomio, por ejemplo f(x)=4x²-5x+6.

Funciones encadenadas

Una función tiene una entrada y una salida, a la entrada la llamamos x y la salida y. La función efectúa operaciones con los valores de entrada para obtener los de salida, a esas operaciones las denotamos por f, siendo la función representada como y=f(x).

Por ejemplo si entran números reales y les hacemos su cuadrado, la función devuelve números reales que son el cuadrado de la entrada. La función es y=f(x)=x²

Supongamos otra función que a cada valor de entrada le suma un 4, y=f(x)=x+4. Una tercera función puede hacer que a cada valor de entrada le calcule su coseno, y=f(x)=cos(x). Ahora podemos encadenar las tres funciones en el orden que se dieron haciendo que cada valor de salida sirva como entrada para la siguiente, entonces el valor de entrada sufre tres cálculos, primero se eleva al cuadrado, luego al resultado se le suma 4, y por último, al resultado se le calcula el coseno, por tanto la función encadenada es: y=f(x)=cos(x²+4)

El orden de encadenamiento es fundamental, así puede salir y=f(x)=cos(x²)+4, o y=f(x)=[cos(x)]²+4, o bien y=f(x)=cos(x+4)². Podemos intentar buscar pares de funciones que al encadenarse en distinto orden dan la misma función. También podemos buscar pares de funciones que al encadenarse devuelven la x de entrada.

La séptima operación

La suma de dos números: 3+4=7
La resta. Conocida la suma y un sumando calcular el otro: 3+x=7 ==> x=7-3=4
La multiplicación de dos números como suma repetida: 3*4=3+3+3+3=12
La división. Conocido el producto y uno de los multiplicandos calcular el otro: 3*x=12  ==> x=12/3=4
La potencia como multiplicación repetida: 3^4=3*3*3*3=81
La raíz. Conocida la potencia y el exponente calcular la base: x^4=81 ==> x=raiz(81;4)=3
Pero queda otra opción, la séptima operación. Conocida la potencia y la base calcular el exponente:3^x=81  ==> es el cálculo del logaritmo de 81 en base 3,
 ¡¡log₃ (81)=4!!

Dos principios: repetición y vuelta atrás

Método de completar el cuadrado

Método
Ecuación de partida ax2+bx+c=0	3x2+5x-2=0 a=3 b=5 c=-2
Paso 1: Dividir por a x2+(b/a)x+(c/a)=0	a=3 x2+(5/3)x-2/3=0
Paso 2: Cambiar el coeficiente de x multiplicando y dividiendo por 2:  2(b/(2a)) x2+2(b/(2a))x+(c/a)=0	x2+(5/3)x-2/3=0 x2+2(5/6)x-2/3=0
Paso 3: Sumar y restar (b/(2a))2 x2+2(b/(2a))x+(b/(2a))2-(b/(2a))2 +(c/a)=0	(b/(2a))2=25/36 x2+2(5/6)x+25/36-25/36-2/3=0
Paso 4: Expresar el cuadrado del binomio (x+b/(2a))2-(b/(2a))2 +(c/a)=0	(x+5/6)2-49/36=0

Una lista de pasos nos permite obtener la expresión del polinomio de segundo grado de la ecuación en función de una sola x. Esto sirve, entre otras cosas para resolver la ecuación.

¿Para qué sirven las Matemáticas?

Está pregunta recurrente surge cuando la motivación para estudiar las Matemáticas, para superar la dificultad que tienen, se ve un poco mermada. El otro día me la hizo Luis en clase de segundo de bachiller. Se puede argumentar que es una preparación que le permitirá entender la técnica y las herramientas profesionales, se le puede argumentar que forma parte de la cultura de la humanidad desde los comienzos de las civilizaciones, se le puede argumentar que resumir, interpretar gráficos, calcular, desarrollar un método, etc, es lo que hace a diario y que las Matemáticas tienen todas esas componentes, pero el caso es que no hay mucho consuelo.
Me dirigí a Luis y le pregunté:
- Cuando desayunas ¿comes galletas con un ritmo constante?
- No, cada vez las como más rápidamente, hasta un punto en que voy cada vez más despacio. - me dijo.
- En su punto más alto, ¿cuántas galletas por minuto eres capaz de comer?. - le volví a preguntar.
- Cuatro. -dijo meditándolo un poco.
- Dime, ¿cuánto tardas en desayunar las galletas y la leche?. -volví a preguntarle.
- Diez minutos. - dijo finalmente.
Fui a la pizarra y argumenté:

•  Suponiendo que la velocidad con la que comes galletas sigue un modelo parabólico, f(x)=ax²+bx+c, al comenzar a desayunar f(0)=0 y al finalizar, f(10)=0. En su punto medio, f(5)=4. Entonces:
• 0=c
• 0=100a+10b+c
• 4=25a+5b+c
• De aquí resolviendo el sistema sale y=(-4/25)x²+(8/5)x
• El número de galletas comidas en función del tiempo F(x)= Integral((-4/25)x²+(8/5)x)=(-4/75)x³+(4/5)x²+C
• Como F(0)=0, entonces, C=0
• Por tanto el número de galletas que comes en 10 minutos es F(10)=-160/3+80=26,6

Se me quedó mirando un rato y exclamó en tono bajo:
- ¡Curioso!.
"Bueno, al menos algo se mueve" -pensé para mis adentros.

Problema con colores

Si intersecamos tres focos de colores, uno rojo, otro azul y otro verde, obtenemos el color amarillo, el fucsia, el azul soralla y el blanco, como se observa en el gráfico. Si al verde le asignamos el número 2, al azul el 3 y al rojo el 5, ¿qué número le corresponde a cada uno de los otros cuatro colores?

Suponemos que 2, 3 y 5 es un indicador del color. Establecemos una medida teniendo en cuenta los valores iniciales dados:
m(verde)=2k
m(azul)=3k
m(rojo)=5k
Si definimos el color de la intersección como el producto de los colores que se superponen, tenemos:
m(azul soraya)=6k²
m(fucsia)=15k²
m(amarillo)=10k²
el blanco se puede considerar como la intersección de los colores primarios, pero, también como interesección de los secundarios:
m(blanco)=30k³=900k⁶;
k³=1/30;
k=raíz cúbica(1/30)  la inversa de la media geométrica de los indicadores de color iniciales
m(blanco)=1

Aprender desde la estructura

Lanzamos una moneda tres veces y anotamos si sale cara o cruz. El espacio muestral es el conjunto de todas las opciones que hay. A estas opciones se les llama sucesos elementales y se pueden representar mediante una lista:

E={ccc, cc+, c+c, +cc, c++, +c+, ++c, +++}

Para construirla hay que seguir un orden, primero ninguna cruz, luego una cruz, luego dos cruces y, finalmente, tres cruces. 
Si fuesen más lanzamientos hay que ser más cuidadoso, habría que ir aumentado, apoyándose en cada opción anterior, añadiéndole cara o cruz:   
ccc;     cccc,ccc+;    ccccc,cccc+,ccc+c,ccc++; .................. 

Sobre esta estructura se pueden buscar los sucesos a estudiar. Por ejemplo, supongamos que lanzamos la moneda tres veces y queremos averiguar la probabilidad de que salgan al menos dos cruces. El suceso lo construimos mirando la lista:

A={c++, +c+, ++c, +++}

Todos los sucesos elementales lanzados con una moneda ideal son igualmente probables. En el suceso A hay 4 opciones, en el espacio muestral hay 8, y la probabilidad de A se mide dividiendo los casos favorables entre los posibles (Laplace), 4/8=0'5.

Describe el barrio

Describe tu barrio según la altura de los edificios.

Suponemos que los edificios está representados en la gráfica.

Tabla de frecuencias:
La variable estadística es la altura que tiene cada edificio.
Hay 6 edificios (n=6) con alturas que van desde 4 hasta 10 (rango=10-4=6).

altura	nº de pisos	frecuencia relativa	porcentaje
4	2	2/6=0'3333	33'33%
6	2	2/6=0'3333	33'33%
8	1	1/6=0'1667	16'67%
10	1	1/6=0'1667	16'67%

Medidas de centralización:
Moda=4 y 6
Altura media=(4x2+6x2+8x1+10x1)/6=6'33
Mediana=6

Buscando motivación

Es posible encontrar matemáticas en todo, entonces, ¿por qué muchos estudiantes no encuentran motivación?
Veamos, ¿qué matemáticas hay en el desayuno que hacemos a diario?:
- Tomamos una traza de café con leche o de cacao con leche.
- Unas galletas o copos.
- Un zumo de naranja.
El café o el cacao supone una cantidad aproximada de unos 200 ml.
Las galletas pueden ser unos 150 g.
El zumo unos 100 ml.
La proporción de café en leche supongamos que es de 1 una parte de café por 5 de leche, 1/5. Ponemos una cuchara sopera de cacao en polvo por taza de leche.
Supongamos que tomamos alrededor de 8 galletas por taza, o bien, tres cucharadas de copos por taza de leche.
La forma de las galletas es rectangular mientras que los copos suelen ser irregulares.  Se supone que la energía de los hidratos de carbono de galletas y copos puede ser semejante.
Las naranjas son aproximadamente redondas y con 3 sacamos los 100 ml. Cada una aporta aproximadamente 33,33 ml.
El 10% de las galletas suelen estar rotas. El 2% de las naranjas suelen estar estropeadas.
El tetrabrik de la leche, el paquete de galletas y el de los copos suelen ser un paralelepípedo.
Cada paquete de galletas da para 5 desayunos.
El tiempo que tardamos en tomar el desayuno es de unos 15 min.
................
La cantidad de vitamina C que tomamos en cada vaso ......
La cantidad de proteínas que hay en la leche .............
La cantidad de grasa que hay en la leche..............
................
Lo que supone de aporte energético con respecto a las necesidades diarias.........
Según la pirámide alimentaria son alimentos que podemos tomar a diario.
Podemos completar el desayuno con ....
Si compramos la marca de cacao X ahorramos .....
...............
El precio del desayuno es de ..........
..............

Ciclo de aprendizaje

El ciclo de aprendizaje queda definido por la siguiente grafica:

Cada fase a su vez sigue un ciclo de aprendizaje que asume una persona.
El ciclo grupal, el que recorre un grupo, tiene estas fases:

1. La motivación procura que se pueda identificar una realidad que hay que superar.
2. La experimentación provoca pequeños gestos de valor que sumados ayudan a resolver el problema y espera que los demás hagan.
3. La conceptualización es el uso de ideas que son eficaces en la resolución.
4. El procesamiento es el esfuerzo que hay que hacer comprobando el funcionamiento de las ideas buscando alcanzar ya objetivos.
5. La mecanización es la técnica, la práctica en la resolución de los problemas siguiendo el modo científico.
6. La consolidación es el habito siguiendo un método, para volver a usar lo que ya hemos visto que sirve.
7. La evaluación es la valoración final de lo que tenemos buscando un criterio para seguir mejorando. El ciclo puede volver a redefinir el problema y volver a realizarse.

La equivalencia en matemáticas (2)

Me preguntan para qué sirven las fracciones equivalentes, aquí va una respuesta:

Supongamos que tenemos dos vasos de limonada simbolizados en el gráfico. Uno tiene dos partes de limón y tres de agua, y el otro, una de limón y dos de agua. Queremos averiguar cuál es el vaso que tiene un  sabor más intenso. En matemáticas simbolizamos la concentración del primero diciendo que el limón que contiene es 2/5 de la cantidad total, y la del segundo, diciendo que el limón que contiene es 1/3 del total. Si dispusiésemos de 3 vasos como el primero y los juntásemos tendríamos que de 15 partes 6 serían de limón, o sea, la cantidad de limón sería 6/15 del total. Si tuviésemos 5 vasos como el pequeño y los juntásemos, también tendríamos 15 partes, de las cuales 5 serían de limón, los 5/15. Y como en ese caso esas cantidades tienen el total igual, 15 partes, ahora podemos comparar la parte del limón, y evidentemente 6 partes da más intensidad de sabor que 5.

2/5=6/15;  1/3=5/15;  2/5>1/3 porque 6/15>5/15

Para eso sirven las fracciones equivalentes.

Función de probabilidad

Tenemos el experimento aleatorio de lanzar dos monedas.
El espacio muestral, el espacio de todos los resultados posibles, es: {(c,c),(c,+),(+,c),(+,+)}
Consideramos la variable aleatoria X=número de caras.
X puede tomar los valores {0,1,2}
El sistema completo de sucesos definidos por la variable X es:
{X=0}={(+,+)}
{X=1}={(c,+),(+,c)}
{X=2}={(c,c)}
La función de probabilidad queda por tanto así:
p(X=0)=1/4
p(X=1)=2/4=1/2
p(X=2)=1/4
La función de probabilidad permite calcular la probabilidad de cualquier suceso definido a través de X. Así:
p(X>=1)=p(X=1)+p(X=2)=1/2+1/4=3/4

¿Dónde hay funciones matemáticas?

Funciones son el objeto del Análisis, desde Newton y Leibnitz se desarrolla esta rama de las matemáticas al poder explicarse los procesos de aproximación infinitesimal.
Tenemos:
Funciones afín y lineal: f(x)=kx, y=ax+b
Funciones exponenciales: f(x)=e^x, f(x)=a^x
Funciones racionales: f(x)=(polinomio)/(polinomio)
Funciones trigonométricas:  f(x)=sen(x), f(x)=cos(x), f(x)=tg(x).
Funciones logarítmicas: f(x)=log(x), f(x)=ln(x)
Función escalera: f(x)=E(x)  (E=parte entera)
Función valor absoluto: f(x)=|x|
Función redondeo inferior: devuelve la parte entera de un número
Función redondeo superior: devuelve la parte entera de un número más uno
Función random: devuelve un número aleatorio (seudoaleatorio)
Función de probabilidad para una variable aleatoria discreta: p(x_i)=a_i

¿Qué es una función matemática?

¿Dónde hay modelos matemáticos?

• En Aritmética encontramos por ejemplo el modelo de la sucesión de Fibonacci:

a₁=1, a₂=1, a_i=a_i-1+a_i-2

• En Análisis encontramos el modelo lineal:

y=ax+b 

• En matemáticas financieras tenemos el modelos de crecimiento acumulado del capital:

C=C₀(1+i)^t  (siendo C₀ el capital final, i el interés y t el tiempo en años)

• En Topología tenemos el modelo de la cinta de Moebius:

¿Qué es un modelo matemático?

¿Dónde hay conceptos en Matemáticas?

En Aritmética tenemos :

• El concepto de número primo, aquel número natural que sólo es divisible por sí mismo y la unidad.
• El concepto de número irracional, como aquel número real que no se puede expresar como fracción.

En Álgebra tenemos:

• El concepto de raíz de un polinomio, como el de aquel número que hace que el valor numérico del polinomio sea cero.
• El concepto de discriminante de una ecuación de segundo grado, la expresión que permite decidir cuantas soluciones va a tener la ecuación.

 En Estadística tenemos:

• El concepto de media, como el parámetro de centralización que se obtiene como suma de todos los datos dividido por el número de ellos.
• El concepto de mediana, como valor de la variable que separa los datos ordenados de la serie estadística por la mitad.

¿Qué es un concepto?

¿Dónde hay fórmulas en Matemáticas?

En Geometría hay muchas fórmulas para calcular áreas o volúmenes:

• El área del cuadrado de lado l es A=l².
• El área del círculo de radio r es A=πr².

En  Estadística también hay muchas fórmulas para calcular parámetros:

• La media de una serie estadística es:

•  La desviación típica de forma abreviada es:

¿Qué es una fórmula matemática?